Duck Chess

[hgm]

Uh? XBoard is a GUI, and it supports is. And XBoard is not any slower than CuteChess, is it?

Cutechess can run games in parallel. It is also easier to configure a tournament.

XBoard can run games in parallell. Just start multiple instances of XBoard.

Configuring a tournament in XBoard is totally trivial. You just click the participants from the engine list, select the type of tournament (round-robin or gauntlet), the number of games per pairing, and press OK. I don't see how that could be done more easily anywhere. Unless CuteChess would decide all by itself what tournament to run...

[JohnWoe]

I'm a lazy programmer and all I want to type is "make all play" and test new version 1000s of games on cutechess. XBoard Blitz games are nice, but real progress comes from playing billions of 1sec games on cutechess.

[JohnWoe]

I think quiescence search searching only normal moves not duck drops. Might be an idea?
Right now I generate ducks in QSearch too.
Since kings can be captured I return checkmate scores from QSearch. Maybe needs improvements?

Maybe duck could always be on board? Let's say sitting on a3. Since it's awkward that first move is different than others. Simplifies code.

[hgm]

I'm a lazy programmer and all I want to type is "make all play" and test new version 1000s of games on cutechess.

You want to type all that! How cumbersome...

With XBoard you would just have to double-click the tourney file.

I still don't see why you wouldn't simply play billions of 1sec games on XBoard.

[hgm]

I think quiescence search searching only normal moves not duck drops. Might be an idea?
Right now I generate ducks in QSearch too.
Since kings can be captured I return checkmate scores from QSearch. Maybe needs improvements?

Maybe duck could always be on board? Let's say sitting on a3. Since it's awkward that first move is different than others. Simplifies code.

Well, start it on a5. No white opening move will be hindered by that. And if white had wanted to block 1... a5 he can still do that on a6. BTW, note that the Duck could be used to deminish the white advantage, by starting it on a square where it blocks white best opening move.

Duck drops are essential in QS. Otherwise you will count on recaptures the opponent won't allow you to make.

[hgm]

I was unhappy with the XBoard version of the Alien Edition; Too many front-end features are broken there.

So I have implemented Duck Chess in the latest regular version now (v4.9.x branch in my on-line repository at http://hgm.nubati.net/cgi-bin/gitweb.cgi ).

[hgm]

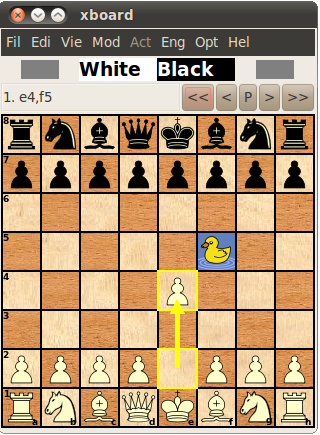
I have now fully written the code for minimaxing the score over Duck move (of opponent) + FIDE move, which is going to replace the usual

if(score > alpha) { score = alpha; if(score >= beta) goto cutoff; }

I am not very happy with it, because it has a significant 'boiler plate' character: I distinguish the cases where there are zero, one or many squares where the move can be blocked. And in each case more or less the same is then done, except that the test for whether a given square could block the move is very different. This is because the test I use for determining whether a distant slider move is blocked at a given square is a bit cumbersome, and it seemed a waste to perform it instead of the very simple test for whether a 'contact move' is blocked (which is just comparing with the single square where it could be blocked), or skipping any test whatsoever (becasue the move was unblockable to begin with). I suppose this could be a form of premature optimization...

Anyway, to test for move blocking I make use of two 240-byte tables, which give me the distance between two squares on the same ray (or 1 for a Knight jump), and a unique code for the direction. I index those by toSqr-fromSqr, as the engine uses 0x88 square numbering (16*rank + file). Before 'looping over Duck locations' I look those up for the move at hand. And I decrement the distance when that move is a capture, as what I really want to know is the number of squares where the move can be blocked. To test whether a Duck location is in the path of the move I then look up the direction for going from fromSqr to duckSqr, and only if it is the same as that of the move I look up the distance between fromSqr and duckSqr. That tells me whether the move can be blocked on duckSqr.

I know ways to do this with less code, but only at the expense of much larger tables, and I am a firm believer of economizing on L1 cache space. The result of the preliminary lookups (done once per move) in any case tell me the number of blocking squares, and when this is 1 I just remember that square, and compare the duckSqr to it in the loop over Duck moves. While in case there are 0 I do the same loop without testing for anything.

The code assumes the previous call to Search returned variables score, exScore and exSqr (the first two already flipped in sign as negamax requires). The latter two are the 'exception' for the single Duck location (at exSqr) where we cannot get the best result because we were not allowed to leave the Duck were we needed it most. For all other Duck locations we can move the Duck to the best location, so they all get the same score 'score'. When there is no exception (because the two best Duck locations have the same effect, which often happens when the best reply cannot be blocked or can be blocked in more than one way), exSqr will be returned as -1. (Which is an invalid square number.)

Each node declares local arrays exScores[], next[] and prev[] indexed by square number (so for me 120 elements, as I use 0x88 numbering), which are going to keep track of the best score so far for each of the 64 Duck locations at the start of the FIDE move. To economize on the effort of updating this we make use of the fact that at least 56 of these Duck locations will result in the same score, namely that of the best move (so far), as moves can be blocked in at most 7 squares, and return a single exceptional score themselves. So we keep up to 8 exceptions in a (circular) doubly-linked list, where the arrays next[] and prev[] hold the links. All Duck locations not in the list will have the same score ('bestScore').

To update the scores array we first run through the list of existing exceptions, and delete any of those which cease to be exceptions because their score is raised to the common score by the current move. This raising can of course only happen when the exception in question would not block the current move. So we have to test for blocking in the loop over Duck locations (i.e. while stepping through the exception list using the next[] links), and this also allows us to keep track of the blocking squares we already have processed (as a bit mask). We also have to test if a Duck location in the exception list is the exception returned by the move (as this will have to use another score in the update), and (when we do encounter it) flag that it already has been updated, by setting exSqr invalid.

After this we then have to loop through remaining blocking squares and the returned exception (if that remained), as these become new exceptions. But they only do so when the move did raise the common score. Which hopefully is not too often, if the move ordering doesn't suck. Of course in that case the common bestScore will also be updated. This whole procedure then gives the best result for each of the 64 possible Duck locations (just before the FIDE move) from all moves that have been searched so far.

Now the opponent will place the Duck in the location with the lowest such score (if he can), or with the second lowest score (in the single case he cannot). So while we are updating the exceptions we also keep track of their minimum. That minimum becomes the 'score' returned by the node, the Duck location that has this score is returned as exSqr, and the second-lowest score as exScore. But the latter two data items are only relevant after all moves have been searched (or we hit a beta cutoff), and are ready to return. In the move loop, however, we do need the lowest score for updating alpha, and deciding whether to take a beta cutoff (if alpha >= beta). That finally gave me the following code:

Code: Select all

        int lowest = beta;
        int moveDir = direct[to-from];                      // direction code (step vector)...
        int moveDist = rayLen[to-from] - (victim != 0);     // ... and length of free path that move traversed
        int k = 8, mask = 0;                                // mask represents squares on ray where Duck could block move
        if(moveDist > 1) {                                  // slider move through 2 or more empty squares
          while((k = next[k]) != 8) {                       // loop through existing exceptions
            int d = dist[to-from];
            if(d > moveDist || direct[k-from] != moveDir) { // move allowed for this Duck location
              if(k == exSqr) {                              // returned exception already existed
                if(exScores[k] < exScore) exScores[k] = exScore;// raise its score if needed
                exSqr = -1;                                 // kludge to flag returned exception is processed
              } else if(score >= bestScore) {
                next[prev[k]] = next[k], prev[next[k]] = prev[k]; // ceases to be exception
                exScores[k] = score;
              } else { // score < bestScore; exceptions remain exceptions, but can still benefit
                if(exScores[k] < score) exScores[k] = score;// raise if needed
              }
              if(exScores[k] < lowest) lowest = exScores[k];
            } else mask |= 1 << d;                          // move blocked, but the blocking does not create a new exception
          }
          if(score > bestScore) {
            mask = (1 << moveDist) - 1 - (mask >> 1);       // find remaining cases of blocking
            if(mask && bestScore < lowest) lowest = bestScore;
            while(mask) {                                   // make all these new exceptions
              int n = BSF(mask);
              k = from + (n + 1)*moveDir;                   // blocking square
              exScores[k] = bestScore;                      // keeps (old) bestScore
              prev[k] = 8; next[k] = next[8];               // add exception to list
              next[8] = prev[next[8]] = k;
              if(k = exSqr) exSqr = -1;                     // forget the returned exception, as it blocks the move.
              mask &= mask - 1;
            }
            if(exSqr >= 0) {                                // the returned exceception did not exist yet, and does not block the move
              exScores[k] = exScore;                        // give it the returned score
              prev[k] = 8; next[k] = next[8];               // and add it to the list
              next[8] = prev[next[8]] = k;
              if(exScore < lowest) lowest = exScore;
            }
            bestScore = score;
          }
        } else if(moveDist == 1) {                          // single blocking square
          int block = from + steps[moveDir-1];              // calculate it (needs not be to-square in case of capture)
          while((k = next[k]) != 8) {                       // loop through existing exceptions
            if(k != block) {                                // move allowed for this Duck location
              if(k == exSqr) {                              // returned exception already existed
                if(exScores[k] < exScore) exScores[k] = exScore;// raise its score if needed
                exSqr = -1;                                 // kludge to flag returned exception is processed
              } else if(score >= bestScore) {
                next[prev[k]] = next[k], prev[next[k]] = prev[k]; // ceases to be exception
                exScores[k] = score;
              } else { // score < bestScore; exceptions remain exceptions, but can still benefit
                if(exScores[k] < score) exScores[k] = score;// raise if needed
              }
              if(exScores[k] < lowest) lowest = exScores[k];
            } else block = -1;                              // move blocked, but the blocking does not create a new exception
          }
          if(score > bestScore) {
            if(block >= 0) {                                // a new exception should be made for the blocked case
              exScores[block] = bestScore;                  // old value!
              prev[block] = 8; next[block] = next[8];       // add exception to list
              next[8] = prev[next[8]] = block;
              if(bestScore < lowest) lowest = bestScore;
            }
            if(exSqr >= 0 && exSqr != block) {              // a new exception should be made for the returned exception
              exScores[exSqr] = exScore;                    // which has its own value!
              prev[exSqr] = 8; next[exSqr] = next8];       // add exception to list
              next[8] = prev[next[8]] = exSqr;
              if(exScore < lowest) lowest = exScore;
            }
            bestScore = score;
          }
        } else {                                            // move cannot be blocked (contact capture)
          while((k = next[k]) != 8) {                         // loop through existing exceptions
            if(k == exSqr) {
              if(exScores[k] < exScore) exScores[k] = exScore;// raise its score if needed
              exSqr = -1;                                   // kludge to flag returned exception is processed
            } if(score >= bestScore) {
              next[prev[k]] = next[k], prev[next[k]] = prev[k]; // ceases to be exception
              exScores[k] = score;
            } else { // score < bestScore; exceptions remain exceptions, but can still benefit
              if(exScores[k] < score) exScores[k] = score;  // raise if needed
            }
            if(exScores[k] < lowest) lowest = exScores[k];
          }
          if(exSqr >= 0) {                                  // a new exception should be made for the returned exception
            exScores[exSqr] = exScore;                      // which has its own value!
            prev[exSqr] = 8; next[exSqr] = next[8];         // add exception to list
            next[8] = prev[next[8]] = exSqr;
            if(exScore < lowest) lowest = exScore;
          }
          if(score > bestScore) bestScore = score;
        }
        if(bestScore < lowest) lowest = bestScore;
        if(lowest > alpha) {
          alpha = lowest;
          if(lowest >= beta) gotoCutoff;
          // stuff for updating or printing PV goes here
        }

[hgm]

I am still wrestling with the concept of a hash move. In 'Refuasal Chess' you must have two moves above beta before you can take a beta cutoff, because one of those would be vetoed. So it would seem reasonable to store the best two moves in the TT there. In Duck Chess more than two moves could be blocked by the Duck. Since one node treats all Duck locations, It must find a refutation for each of those before you can take a beta cutoff. If a move scores above beta, it refutes at least 56 Duck locations, as it can be blocked in only 7 places, and there might be an 8th place where the moves itself scores lower because of duckzwang.

But at the moment I see no argument that excludes that each of the possibly 8 exceptions will not need a different move to refute them.

Any ideas?

[JohnWoe]

These duck moves increase the branching factor quite a lot. But still every possible duck drop needs to be searched. I tried to hash best duck drop in TT and search that in full depth but that didn't work. I think the best strategy is some kind of NN for best duck drops and search that in full depth.
I managed to compile XBoard but no duck variant. My engine is UCI so polyglot won't support it anyway.

I tried to always place duck on board but. That changed perft. As if the duck is on e5. White has 20 * (20 + 39) moves. But black can't place duck on e5...

[hgm]

Duck Chess should be selectable from the New Variant menu, at the bottom of third column of buttons. If not, you compiled a wrong version.

And of course you have to use UCI2WB as adapter, not Polyglot.