For an Opening Book I want to use the elo information of the players
So lets say in a certain position 2 moves exist in a pgn to be parsed, I would weigh the two moves according to the probability of either player winning in a 1vs1 tournament.
E = 1 / (1 + 10 ^ ( ( EloB - EloA ) / 400 ) )
So this should work easily.
But what can I do if there is more than one possible move.
is there a simple way to estimate the chance of one person winning in a tournament versus several opponents?
Elo Calcuation
Moderator: Ras
-
MattieShoes
- Posts: 718
- Joined: Fri Mar 20, 2009 8:59 pm
Re: Elo Calcuation
Couldn't you just sort of simulate a RR tourney and add up the expected score for each matchup, divide it by the # of rounds? Then you'd get the expected score for each participant.
Say, 2700+2600+1900
2700 would have (.64 + .99) / 2 = .82
2600 would have (.36 + .98) / 2 = .67
1900 would have (.01 + .02) / 2 = .01
Say, 2700+2600+1900
2700 would have (.64 + .99) / 2 = .82
2600 would have (.36 + .98) / 2 = .67
1900 would have (.01 + .02) / 2 = .01
-
Laskos

- Posts: 10948
- Joined: Wed Jul 26, 2006 10:21 pm
- Full name: Kai Laskos
Re: Elo Calcuation
Yes, but what's the probability of the 2600 participant to win the tourney in say 4 games each RR? In 100 games tourney? It's a little bit tricky, brute force Monte Carlo would solve, but I would try to think at a more beautiful (analytic) solution.MattieShoes wrote:Couldn't you just sort of simulate a RR tourney and add up the expected score for each matchup, divide it by the # of rounds? Then you'd get the expected score for each participant.
Say, 2700+2600+1900
2700 would have (.64 + .99) / 2 = .82
2600 would have (.36 + .98) / 2 = .67
1900 would have (.01 + .02) / 2 = .01
Kai
-
towforce

- Posts: 12695
- Joined: Thu Mar 09, 2006 12:57 am
- Location: Birmingham UK
- Full name: Graham Laight
Re: Elo Calcuation
This could be done by summing the probabilities of each possible way for each player to get a particular tournament score. Some similar (but not exactly the same) calculation was done in this thread on CTF.Laskos wrote:Yes, but what's the probability of the 2600 participant to win the tourney in say 4 games each RR? In 100 games tourney? It's a little bit tricky, brute force Monte Carlo would solve, but I would try to think at a more beautiful (analytic) solution.MattieShoes wrote:Couldn't you just sort of simulate a RR tourney and add up the expected score for each matchup, divide it by the # of rounds? Then you'd get the expected score for each participant.
Say, 2700+2600+1900
2700 would have (.64 + .99) / 2 = .82
2600 would have (.36 + .98) / 2 = .67
1900 would have (.01 + .02) / 2 = .01
Human chess is partly about tactics and strategy, but mostly about memory
-
Edmund
- Posts: 670
- Joined: Mon Dec 03, 2007 3:01 pm
- Location: Barcelona, Spain
Re: Elo Calcuation
Thanks for the contributions so far.
Yesterday I had a long discussion with Pradu about the topic and he brought me onto a different solution.
Rather to look at the ratings of the players who played the alternative moves and thus determine the weight for one particular move, he suggested, that the first step should be to calculate the winning probability of a certain move, looking at the outcome regarding against who it was played.
For example, if a player with +200 elo difference wins with a certain move, the move will probably be weaker, than if a -200 elo player won with it.
So for the calculation he proposed an optimization:
sum(Error_i) = sum(abs(Result_i - ELO_to_Winprobability(EloDiff_i + EloMove)))
sum(Error_i) -> 0
and EloMove is the solution
Having an EloMove one could easily use it to weigh against the other EloMoves, by converting them to Winprobabilities.
The main problem I have is the Optimization Process. Can anyone see some approximation for it? Otherwise the process would be painfully slow. Or any other suggestions?
Concerning the formula, leaving away the abs():
0 = sum(Result_i - ELO_to_Winprobability(EloDiff_i + EloMove))
0 = sum(Result_i) - sum(ELO_to_Winprobability(EloDiff_i + EloMove))
sum(Result_i) = sum(ELO_to_Winprobability(EloDiff_i + EloMove))
sum(Result_i) = sum(1 / (1 + 10 ^ ( ( EloDiff_i + EloMove) / 400 ) ) )
sum(Result_i) = sum(1 / (1 + 10^(EloDiff_i/400) * 10^(EloMove/400) ) )
we didn't manage to simplify it any further. Note that calculating sum(Result_i) is easy, but the second part is much more complicated to evaluate, as I would have to save the EloDiff for each position.
Yesterday I had a long discussion with Pradu about the topic and he brought me onto a different solution.
Rather to look at the ratings of the players who played the alternative moves and thus determine the weight for one particular move, he suggested, that the first step should be to calculate the winning probability of a certain move, looking at the outcome regarding against who it was played.
For example, if a player with +200 elo difference wins with a certain move, the move will probably be weaker, than if a -200 elo player won with it.
So for the calculation he proposed an optimization:
sum(Error_i) = sum(abs(Result_i - ELO_to_Winprobability(EloDiff_i + EloMove)))
sum(Error_i) -> 0
and EloMove is the solution
Having an EloMove one could easily use it to weigh against the other EloMoves, by converting them to Winprobabilities.
The main problem I have is the Optimization Process. Can anyone see some approximation for it? Otherwise the process would be painfully slow. Or any other suggestions?
Concerning the formula, leaving away the abs():
0 = sum(Result_i - ELO_to_Winprobability(EloDiff_i + EloMove))
0 = sum(Result_i) - sum(ELO_to_Winprobability(EloDiff_i + EloMove))
sum(Result_i) = sum(ELO_to_Winprobability(EloDiff_i + EloMove))
sum(Result_i) = sum(1 / (1 + 10 ^ ( ( EloDiff_i + EloMove) / 400 ) ) )
sum(Result_i) = sum(1 / (1 + 10^(EloDiff_i/400) * 10^(EloMove/400) ) )
we didn't manage to simplify it any further. Note that calculating sum(Result_i) is easy, but the second part is much more complicated to evaluate, as I would have to save the EloDiff for each position.
-
Edmund
- Posts: 670
- Joined: Mon Dec 03, 2007 3:01 pm
- Location: Barcelona, Spain
Re: Elo Calcuation
Would this make any sense?
Calculate the average difference between the expected score and the actual score for each move:
Move_Win% = (Sum(Result) - Sum(Expected_Win%)) / Number_of_games
then Move_Win% would be on a scale between -1 and +1 depending on how well it influenced the final outcome:
-1 = All games should have been won considering Elo difference, but the move was so bad, that all of them were lost
0 = The games ended like the Elo difference would have suggested
+1 = All games should have been lost considering Elo difference, but the move was so good, that all of them were won.
I can now use this score to weigh this move linearly against the scores of the other moves. Or is any other weighting appropriate?
Calculate the average difference between the expected score and the actual score for each move:
Move_Win% = (Sum(Result) - Sum(Expected_Win%)) / Number_of_games
then Move_Win% would be on a scale between -1 and +1 depending on how well it influenced the final outcome:
-1 = All games should have been won considering Elo difference, but the move was so bad, that all of them were lost
0 = The games ended like the Elo difference would have suggested
+1 = All games should have been lost considering Elo difference, but the move was so good, that all of them were won.
I can now use this score to weigh this move linearly against the scores of the other moves. Or is any other weighting appropriate?
-
MattieShoes
- Posts: 718
- Joined: Fri Mar 20, 2009 8:59 pm
Re: Elo Calcuation
It sounds like you're doing almost exactly what I'm doing.  I also added two weighting factors in mine too.
I also added two weighting factors in mine too.
I decided to give higher weight to games between near equal players. Kasparov can play 1. a3 against my engine all day and he's going to win them all -- that doesn't make 1. a3 a good opening. Basically, very different ratings yields very little useful information about the quality of an opening.
I also decided to give higher weight to games between higher rated players, since fishy openings are more likely to be punished by a good player.
So I came up with something like this:
weight = (avgRating/2000)^2 * MIN(expectedScore, 1-expectedScore)*2
Then I multiply frequency and strength numbers by the weight.
2000 vs 2000 would have a weight of about 1.00.
2400 vs 2400 would have a weight of about 1.44.
2800 vs 2800 would have a weight of about 1.96.
2800 vs 2600 would have a weight of about 1.00.
2800 vs 2400 would have a weight of about 0.31.
2400 vs 2000 would have a weight of about 0.22.
I just made up the formula and haven't tested it in any sort of rigorous manner, but it seems to work okay. It's probably because of the pgn file I used to build the book, but it does seem to like 1. c4 more than it should though
The weights end up looking like this
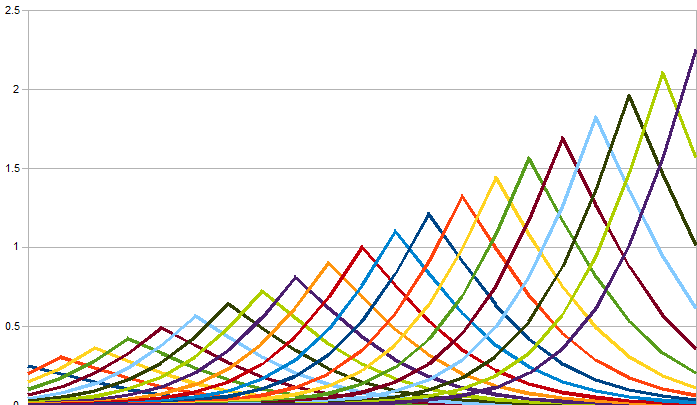
I decided to give higher weight to games between near equal players. Kasparov can play 1. a3 against my engine all day and he's going to win them all -- that doesn't make 1. a3 a good opening. Basically, very different ratings yields very little useful information about the quality of an opening.
I also decided to give higher weight to games between higher rated players, since fishy openings are more likely to be punished by a good player.
So I came up with something like this:
weight = (avgRating/2000)^2 * MIN(expectedScore, 1-expectedScore)*2
Then I multiply frequency and strength numbers by the weight.
2000 vs 2000 would have a weight of about 1.00.
2400 vs 2400 would have a weight of about 1.44.
2800 vs 2800 would have a weight of about 1.96.
2800 vs 2600 would have a weight of about 1.00.
2800 vs 2400 would have a weight of about 0.31.
2400 vs 2000 would have a weight of about 0.22.
I just made up the formula and haven't tested it in any sort of rigorous manner, but it seems to work okay. It's probably because of the pgn file I used to build the book, but it does seem to like 1. c4 more than it should though
The weights end up looking like this

-
Laskos

- Posts: 10948
- Joined: Wed Jul 26, 2006 10:21 pm
- Full name: Kai Laskos
Re: Elo Calcuation
It is easier to establish rules of thumb for such tourneys with an error margin of say 1-3%. The scores would obey a normal distribution due to central limit theorem for sufficiently large amount of games. For a normalized normal distributions we have only two parameters, the central value and the width (the width will be, for a normalized normal distribution, proportional to 1/Sqrt(Number of Games)). In RR tourneys the width and normalization would be the same for all engines, so we just have to count the overlap of the distributions to derive the chances of win in the tourney (Erf function). It will be prone to errors for very few RR games (not exactly normal distribution, and the overlap is not symmetrical). If I have a spare hour, I would try to give a rule of thumb formula for calculating the probability of win for a number A of engines with predefined Elo values in a number B of Round Robin games, I don't think it's hard, I just need some constants.towforce wrote:This could be done by summing the probabilities of each possible way for each player to get a particular tournament score. Some similar (but not exactly the same) calculation was done in this thread on CTF.Laskos wrote:Yes, but what's the probability of the 2600 participant to win the tourney in say 4 games each RR? In 100 games tourney? It's a little bit tricky, brute force Monte Carlo would solve, but I would try to think at a more beautiful (analytic) solution.MattieShoes wrote:Couldn't you just sort of simulate a RR tourney and add up the expected score for each matchup, divide it by the # of rounds? Then you'd get the expected score for each participant.
Say, 2700+2600+1900
2700 would have (.64 + .99) / 2 = .82
2600 would have (.36 + .98) / 2 = .67
1900 would have (.01 + .02) / 2 = .01
To do it more rigorously (without assuming a normal distribution, for example) is much harder, Monte Carlo is what comes to my mind. Anyway, if I post here some results, I would be happy for them to be checked by a Monte Carlo simulation.
Kai
-
hgm

- Posts: 28426
- Joined: Fri Mar 10, 2006 10:06 am
- Location: Amsterdam
- Full name: H G Muller
Re: Elo Calcuation
The problem is that the engine you want to calculate the winning probability of has to be compared to the maximum of the score of its competitors. Ad there usually are only a small number of serious competitors, even in a large round-robin. The distribution of the maxium of a small number of normally distributed variables is not very Gaussian.
-
MattieShoes
- Posts: 718
- Joined: Fri Mar 20, 2009 8:59 pm
Re: Elo Calcuation
Y'all passed my math level.  So given infinite games, the numbers I had would be correct, yes? And as the number of games decreases, noise from the odd bad/great games increase... Wouldn't one have to figure out a formula to predict the number of draws in a non-infinite scenario?
So given infinite games, the numbers I had would be correct, yes? And as the number of games decreases, noise from the odd bad/great games increase... Wouldn't one have to figure out a formula to predict the number of draws in a non-infinite scenario?
But given the context here, an opening book, is it really necessary to go through all that?
I'm thinking one could take a page out of IMDB.com's book with their movie rankings.
1) ignore any moves with less than N results
2) adjust the scores of each move like this
That'd push moves with few data points towards the average, and as more points are collected, they'd approach their raw score.
Then one just has to pick a reasonable N...
But given the context here, an opening book, is it really necessary to go through all that?
I'm thinking one could take a page out of IMDB.com's book with their movie rankings.
1) ignore any moves with less than N results
2) adjust the scores of each move like this
Code: Select all
adjustedScore = score * freq/(freq+N) + average * N/(freq+N)Then one just has to pick a reasonable N...