Let's define this schizophrenic Leela engine by the scores regular engines get against it as:
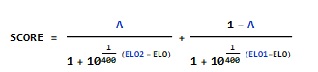
(1)
Here SCORE is the score a regular engine gets in a match against Leela, ranging from 0 (0%) to 1 (100%).
A is the the degree of schizophrenia of Leela, closer to 0.5 is more accentuate double personality, closer to 0 or 1 means less schizophrenia (range ids from 0 to 1).
ELO is the Elo of regular engine.
ELO1 and ELO2 are defining personalities of Leela, 2 personalities.
We define the Elo_of_Leela in a pool of regular engines as an Elo of regular engine against which it scores exactly 1/2 (50%).
Setting SC0RE=0.5 and solving for Elo, we get Elo_of_Leela as a function of ELO1, ELO2 and A:

(2)
Given the score a regular engine gets against Leela, it's hard to derive immediately the Elo of that regular engine in a pool of regular engines. We have, given the score, to derive ELO as a function of SCORE, ELO1, ELO2, A from equation (1). Against regular engines, Elo as a function of score is given by simple logistic inversion. Here the solution for Elo of regular engine is:

(3)
Now one can check the model, by fitting parameters A, ELO1, ELO2 to empirical data. The model is invariant to Elo translations, only Elo differences count, so basically we have only 2 variables in the model.
The best empirical data (rating list of regular engines) at short time control on large Elo span I found are here:
http://fastgm.de/60-0.60.html
The ratings are calculated by Ordo, so they do not suffer from any compression or distortion of BayesElo. Also, the error margins are small. Time control id 60'' + 0.6''.
I used 7 datapoints from this list, from the weakest, Ethereal 8.16 to the strongest, Stockfish 10. For each datapoint (7 different regular engines), I played 1000 games of Leela (one of the latest of test30 nets) against them.
Warning: the time control used in these games was very short, 6'' + 0.1''.
The fit of the model on 7 datapoints on very large Elo span gave (from equation (3)):
A = 0.53 (close to 0.5, very schizophrenic Leela)
ELO1 - ELO2 = 1070
Basically, Leela has two personalities of similar importance in matches, differing by about 1000 Elo points.
If I choose ELO1 equal to 3500, then ELO2 is 2430.
From the equation (2), the Elo_of_Leela is 3071 Elo points. It can be translated to anything by just translating ELO1, ELO2, but keeping their difference constant. I will keep those values, translating the rating list of Andreas (fastgm), and see how the fit works.
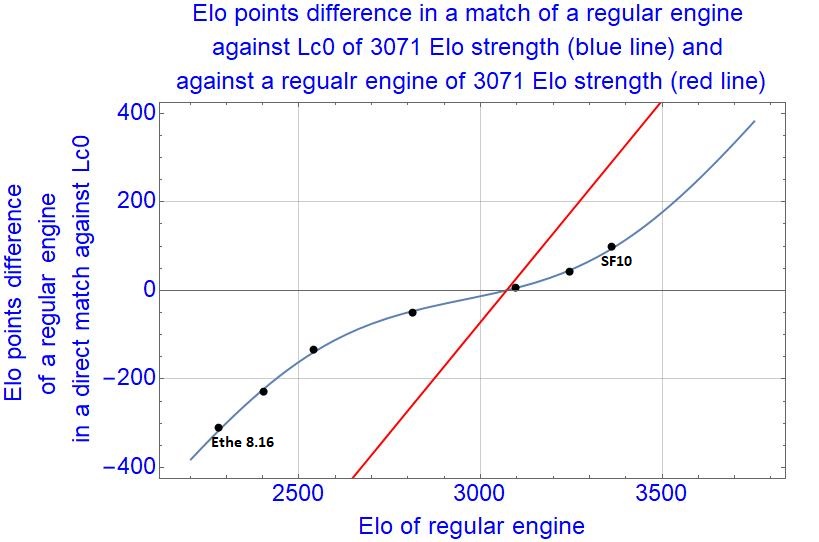
Each black datapoint is given by 1000 ultra-fast games match for each regular engine against Leela. The fit is almost perfect, with just 2 parameters fitting 7 datapoints. So, a double personality of Leela seen by regular engines is in almost perfect agreement with scores one gets when playing different rated regular engines against it. Again, Leela could be given an "Elo_of_Leela", but Leela doesn't obey the Elo logistic model of regular engines. So, in rating lists, Leela's rating may be almost arbitrary, depending on opponents. If you give here weak opponents, she would be rated lower, if we give here strong opponents, she would be rated higher. The "Elo compression" when a regular engine plays Leela is very pronounced, especially on small to medium Elo spans.
The two personalities on fairly strong GPU and reasonable time control can be defined as: one super-strong, well above any regular engine. Another the level of a mediocre regular engine. I do not know if double personality is expressed mostly in matches of games or in each game, move by move.
The only warning is that TC I used was very short.
If humans resemble Leela in playing, as many argue, including me, humans too seem schizophrenic to regular engines. The Elo ratings of humans in a pool of regular engines will be compressed, and the best a human can do is to play the best engine to improve his rating. If say top 5 engines with their CCRL ratings are introduced in human FIDE pool, they will inflate the general FIDE human ratings, and the top GMs would better play only engines to improve their FIDE rating. Probably a similar plot can be made of a human playing in a pool of regular engines, but no human will play thousands of games against strong engines in FIDE conditions to have enough empirical data.
